Quand on débute en électronique, que ce soit avec un Raspberry Pi ou un Arduino, on se trouve rapidement confronté au calcul des résistances. Que ce soit pour alimenter une LED, polariser un transistor ou autre… on a toujours besoin de faire un calcul.
Quand on débute en électronique, que ce soit avec un Raspberry Pi ou un Arduino, on se trouve rapidement confronté au calcul des résistances. Que ce soit pour alimenter une LED, polariser un transistor ou autre… on a toujours besoin de faire un calcul.
Manu, un fidèle lecteur (et intervenant) du blog et du forum a concocté cette Pi-ramide qui vous rappellera « sur le pouce » les formules dont vous avez besoin.
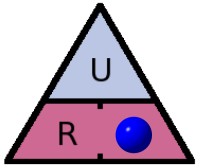
Une Pi-ramide pour des équations d’électricité
Si certains pensent que les Égyptiens de l’antiquité connaissaient l’électricité, c’est surtout leurs connaissances en géométrie que l’on retrouve dans la construction des pyramides.
C’est ce solide que Manu a retenu pour créer un aide mémoire à l’usage des électroniciens débutants.
Comment ça marche ?
C’est tout simple ! On va prendre un exemple…
C’est tout pareil !
Toutes les faces de la pyramide fonctionnent de la même façon !
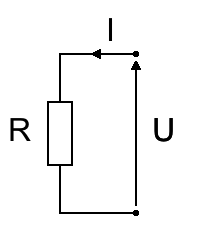
Ici on voit à droite P et R ainsi que I2 : P c’est la puissance en watts, R et I on les a vus juste avant.
Alors quelle doit être la puissance de la résistance dans l’exemple précédent ? (c’est pour éviter qu’elle n’émette des signaux de fumée avant de rendre l’âme)
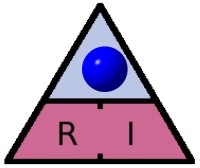
Je cherche P => je mets le pouce dessus il reste ??? R x I2
R on a dit 180 Ω (c’est celle que j’avais en stock) et un courant de 10 mA (0,010 A) =>
P = 180 x 0,01 x 0,01 = 0,018 watt
Pas de souci une résistance 1/4 watt (250 mW) fera l’affaire puisque la puissance dissipée n’est que de 18 mW. Par sécurité prévoyez toujours une puissance au moins double de la puissance nécessaire.
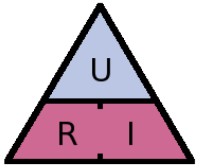
Et en fonction de la face que vous choisissez, vous avez une de ces 4 formules :
- P = U x I
- U = R x I
- P = R x I²
- P = U² / R
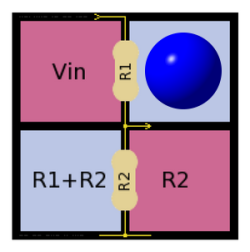
Et le carré en dessous de la Pi-ramide ?
Ah oui c’est vrai il y a un carré sous la Pi-ramide ! J’ai failli oublier de vous en parler 
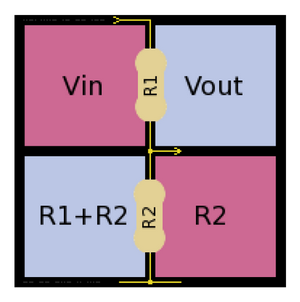
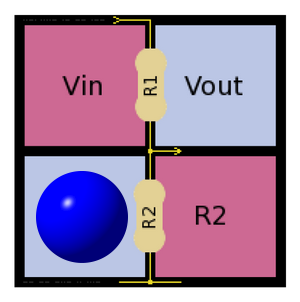
Celui-là concerne le pont diviseur de tension :
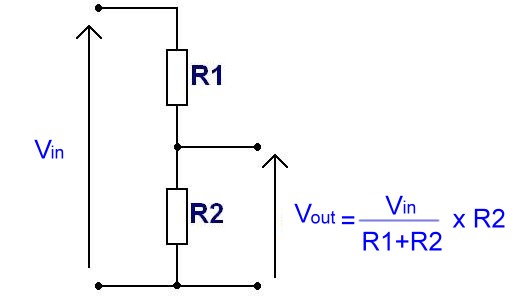
Une tension d’entrée Vin est appliquée au pont diviseur constitué par 2 résistances, R1 et R2. Il permet de récupérer en sortie Vout, qui est une partie de la tension d’entrée.
Exemple de pont diviseur
 Bon, cette fois on a un capteur (de ce que vous voulez
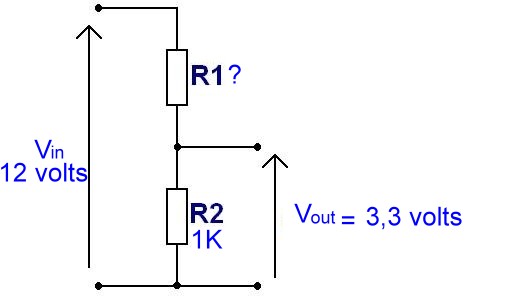
Bon, cette fois on a un capteur (de ce que vous voulez  ) qui sort soit rien (0 volt) soit du 12 volts (niveau 1). On ne peut pas envoyer sa sortie sur un port GPIO du Raspberry Pi. Un GPIO supporte au maximum 3,3 volts !
) qui sort soit rien (0 volt) soit du 12 volts (niveau 1). On ne peut pas envoyer sa sortie sur un port GPIO du Raspberry Pi. Un GPIO supporte au maximum 3,3 volts !
On va utiliser un pont diviseur pour ramener la tension d’entrée (12 volts) à 3,3 volts. J’avais en stock une résistance de 1KΩ qui fera l’affaire pour R2. Bon, et je mets quoi pour R1 ???
Bin… pour vérifier on va faire le calcul dans l’autre sens si vous voulez bien ! reprenez le pont diviseur vu précédemment avec
R2 = 1KΩ et R1 = 2.7 KΩ
Je vous laisse faire le calcul… on trouve Vout = 3,24 volts
ensuite on prend R2 = 1KΩ et R1 = 2.2 KΩ
on refait le calcul et on trouve Vout = 3,75 volts
Alors vous prenez quoi, vous ?
tadaaaa ! Moi je prendrai R1 = 2.7 KΩ car la tension de 3,24 volts est compatible avec les ports GPIO vu qu’elle est inférieure (très peu) à 3,3 volts.
Si je mets la résistance de 2,2 KΩ, la tension de 3,75 volts va dépasser la limite de 3,3 volts et mon port GPIO risque d’être détruit, si je n’ai pas de bol c’est le CPU qui va cesser de fonctionner… Et un Raspberry Pi sans microprocesseur c’est ??? Bon à mettre à la poubelle (pensez au recyclage ! )
Les puristes vous diront que ce n’est pas bien d’abaisser la tension avec un pont diviseur pour attaquer un GPIO. Ils vous recommanderons d’utiliser un convertisseur de tension, beaucoup plus sûr. Ils ont raison !! Mais le pont diviseur fonctionne très bien si vous êtes certain(e) de la tension du capteur.
Retenez la méthode qui consiste à refaire le calcul « dans l’autre sens ». Ça permet de s’assurer que la valeur trouvée est cohérente et que les calculs son justes.
Un exercice pour voir si vous avez compris
Pour finir je vous propose un exercice pour voir si vous arrivez à vous débrouiller… (attention il y a peut-être un piège  … ou pas) :
… ou pas) :
Vous avez un pont diviseur constitué de 2 résistances R1 = 2,2 KΩ et R2 = 5,6 KΩ. La tension de sortie Vout doit être de 5 volts… Vous envoyez combien sur Vin ?
Prenez votre temps, faites votre calcul, vérifiez en refaisant le calcul « à l’envers ». Quand vous serez certain(e) que votre résultat est bon, ouvrez ce PDF qui vous propose la solution 
Comment réaliser cette pyramide ?
Méthode 1 : couper-coller
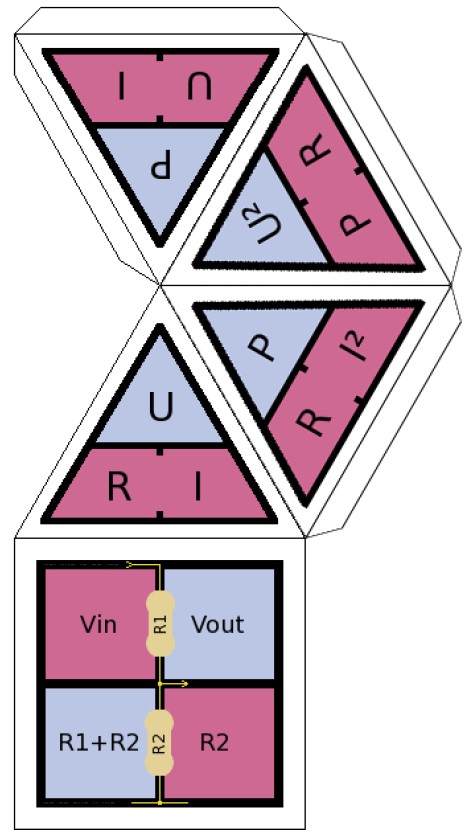 Manu vous facilite la tâche : il a réalisé un modèle de pyramide que vous pouvez découper. C’est celui que j’ai utilisé. Il y a même les rabats pour le collage. Téléchargez ce fichier PDF et imprimez le.
Manu vous facilite la tâche : il a réalisé un modèle de pyramide que vous pouvez découper. C’est celui que j’ai utilisé. Il y a même les rabats pour le collage. Téléchargez ce fichier PDF et imprimez le.
Méthode 2 : Le Python
Pour ceux qui voudraient fabriquer leur propre Pi-ramide, Manu a écrit un programme Python qui calcule les différentes dimensions de l’objet :
#!/usr/bin/python2.6
# -*- coding: utf-8 -*-
def Pythagore (a,b,c):
#=============
# Affiche la valeur des côtés du triangle rectangle
# a et b sont les côtés adjacent à l'angle droit
# c est le côté opposé à l'angle droit, l'hypoténuse
#=============
print " a = %s \n b = %s \n c = %s" % ( str(a), str(b), str(c) )
#=============
# "a" est la valeur à chercher
#=============
if type(a) == type('str'):
a = ( c**2 - b**2 ) ** .5
print "a = %f \n" % a
return a
#=============
# "b" est la valeur à chercher
#=============
if type(b) == type('str'):
b = ( c**2 - a**2 ) ** .5
print "b = %f \n" % b
return b
#=============
# "c" est la valeur à chercher 'hypoténuse'
#=============
if type(c) == type('str'):
c = ( a**2 + b**2 ) ** .5
print "c = %f \n" % c
return c
#
# Valeurs des côtés de la pyramide
#
cote_base = 10 # base en carré
cote_base_sommet = 10 # arrêtes vers le sommet
#
# Longueur de la diagonale sur la base
#
print "\nDiagonale base :"
diagonale_base = Pythagore ( cote_base , cote_base , "?" )
#
# Centre pyramide par rapport à la diagonale base
#
print "\nCentre de la pyramide sur la diagonale :"
centre_hauteur_diagonale = diagonale_base / 2
print centre_hauteur_diagonale
#
# Hauteur de la pyramide
#
print "\nHauteur de la pyramide :"
hauteur_pyramide = Pythagore ( "?" , centre_hauteur_diagonale , cote_base_sommet )
#
# Centre pyramide par rapport à un côté de la surface de base
#
print "\nCentre de la pyramide sur le coté :"
centre_hauteur_cote = cote_base / 2
print centre_hauteur_cote
#
# Hauteur sur face incliné de la pyramide
#
print "\nhauteur sur plan face incliné :"
hauteur_face_incline = Pythagore ( centre_hauteur_cote , hauteur_pyramide , "?")
Conclusion
Avec la Pi-ramide de « Tout en carton » sur votre établi, finis les oublis de formule. C’est un outil que vous pouvez laisser traîner sans crainte des court-circuits ou de l’usure des batteries…
Un jour vous n’en aurez plus besoin. Vous aurez intégré ces formules. Mais vous vous souviendrez de cette Pi-ramide qui vous a aidé à démarrer 
Cet article ne tient pas compte des résistances présentes en parallèle sur l’entrée ou la sortie du pont… C’est une autre histoire 



 ) et un courant de 10 mA (0,010 A) parcourt la LED (ça aussi c’est dans la doc (là, j’insiste
) et un courant de 10 mA (0,010 A) parcourt la LED (ça aussi c’est dans la doc (là, j’insiste 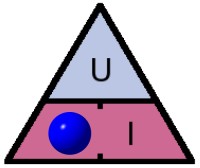
 )Allez on calcule R = 1,7 / 0,010 = 170 Ω
)Allez on calcule R = 1,7 / 0,010 = 170 Ω